Om de locatie van een bepaald punt nauwkeurig te kunnen definiëren, kwamen ingenieurs op het idee om coördinatensystemen te maken. Deze systemen zouden informatie met betrekking tot topologie bevatten, die in feite verwijst naar elke vorm van geografische correlaties die de nauwkeurige definitie van de centrum- en asrichting van het systeem garanderen, evenals informatie met betrekking tot het metrische systeem en de gebruikte meeteenheden. Er zijn tegenwoordig twee hoofdcategorieën coördinatensystemen, waarvan de eerste de oudste is en bekend staat als het geografische coördinatensysteem. In deze blog zullen we ons echter concentreren op de tweede categorie, genaamd Flat Coordinates System.
Het platte coördinatensysteem, dat ook een orthogonaal of rechthoekig coördinatensysteem wordt genoemd, is ook een vrij oud systeem, althans wat betreft zijn basisvorm die al eeuwen wordt gebruikt. Dit is het perfecte type coördinatensysteem voor de precieze definitie en nauwkeurige meting van de locatie van geografische entiteiten die zich op het oppervlak van een vlakke projectie van de aarde bevinden. Het platte coördinatensysteem in zijn moderne vorm komt voort uit het Cartesiaanse coördinatensysteem, wat redelijk is om te zeggen, gezien de overeenkomsten in geometrische attributen en de benadering van het ontwerp van het systeem in het algemeen. Laten we een paar woorden delen met betrekking tot Cartesiaanse coördinaten, het systeem op basis waarvan de oprichting van het platte coördinatenstelsel is voltooid.
Cartesiaanse coördinaten
Het Cartesiaanse coördinatensysteem is eigenlijk een wiskundige structuur die voornamelijk bestaat uit een startpunt in 3D-ruimte met een bekende locatie, en een specifieke meeteenheid voor afstanden in het metrische systeem dat wordt gebruikt bij het ontwerp van het systeem. Twee assen (Ox, Oy) langs het Oxy-vlak zijn zo gemaakt dat ze beide het bekende startpunt van het systeem kruisen en verticaal op elkaar zijn gericht. De Ox- en Oy-assen worden vaak verdeeld in kleinere meeteenheden die op de projectie worden gedemonstreerd op een manier die het doel van de waarnemer verbetert om metrische informatie te extraheren door naar de kaart te kijken.
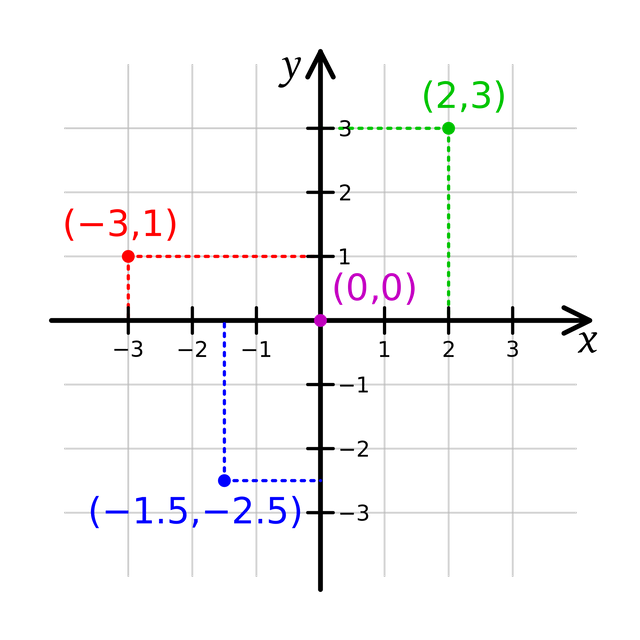
2D Cartesiaans coördinatensysteem. / Afbeeldingsbron: commons.wikimedia.org ( Public Domain Dedications (Author: Kbolino )
Dezelfde soort referentiesystemen voor analyse van ruimtelijke distributie worden voornamelijk gebruikt bij het ontwerp en de constructie van grafische weergaven. Tijdschriften of kranten bieden bijvoorbeeld vaak statistische grafieken met betrekking tot verschillende enquêtes, dus het is veilig om te zeggen dat het in deze gevallen volledig aan de waarnemer is om alle beschikbare en aangetoonde informatie te absorberen met behulp van die grafische elementen. Natuurlijk draagt de auteur, die in ons geval eigenlijk een cartograaf is, de verantwoordelijkheid om informatie beschikbaar, gemakkelijk te begrijpen en voor het oog zichtbaar te maken. Efficiënte analyse van de ruimtelijke verdeling door het ontwerp en gebruik van het juiste referentiesysteem is het hoofddoel; Het Cartesiaanse coördinatenstelsel was wat nodig was. Het werk van cartografen hangt wereldwijd af van dit systeem.
Cartografen gebruiken het Cartesiaanse coördinatensysteem eigenlijk als een gids en een basis voor het opzetten en definiëren van de verschillende coördinatensystemen die in mappings worden gebruikt, om alle berekeningen te vereenvoudigen die nodig zijn voor de afronding van dit proces. De verschillen in het berekeningsproces tussen het oppervlak van de projectie en het oppervlak van de referentiebol zijn triviaal in geval van conforme projecties, maar Cartografen moeten mogelijk verschillende coördinatensystemen gebruiken afhankelijk van het vereiste precisieniveau voor berekeningen. Het is de moeite waard om in gedachten te houden dat hoe groter het gebied van het natuurlijke aardoppervlak dat wordt afgebeeld op een projectie, hoe lager het niveau van precisie dat kan worden bereikt. Met andere woorden,
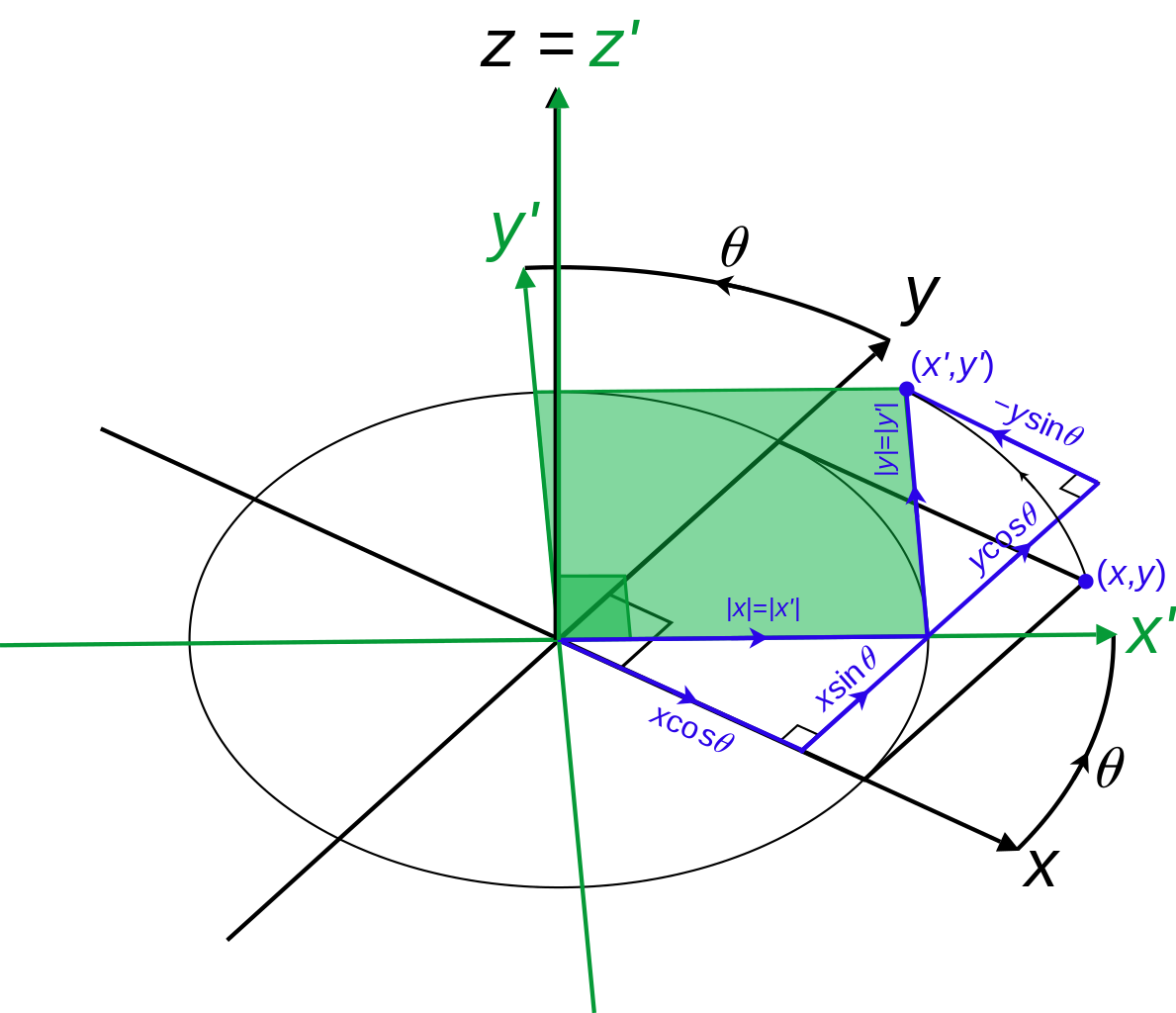
Rotatietransformatie van Cartesiaanse coördinaten./ Afbeeldingsbron: commons.wikimedia.org ( Creative Commons CC0 1.0 Universal Public Domain Dedication (Auteur: Maschen )
Platte coördinaten
Op een oppervlak van een hypothetisch oneindig gebied kan men geen enkel soort referentiepunt vinden of vaststellen zonder het gebruik van een Cartesiaans coördinatenstelsel. Het noodzakelijke referentiepunt kan worden gespecificeerd en genoteerd als het punt waarop de primaire assen van het systeem elkaar kruisen. Ons systeem wordt vervolgens vastgesteld door het Oxy-vlak in vierkanten te verdelen, wat wordt bereikt met de gravure of op gelijke afstand, absoluut parallelle lijnen die de assen verticaal snijden. Na het maken van het kaartraster als resultaat van het hierboven beschreven proces, zijn cartografen nu in staat om de coördinaten van elk specifiek punt nauwkeurig te definiëren in relatie tot de gegeven locatie van het referentiepunt.
Om de coördinaatwaarden ( X , Y ) te berekenen , meten ingenieurs de afstand van elk specifiek punt tot beide assen, terwijl elke meting verwijst naar de afstand vanaf een van de twee assen en plaatsvindt in de richting parallel aan de andere as. De coördinaatwaarden worden vervolgens berekend door de gemeten afstanden in de maateenheden van het raster uit te drukken en rekening te houden met het vereiste nauwkeurigheidsniveau. Horizontale afstanden worden weergegeven door de waarde van de variabele X , terwijl verticale afstanden of variaties van de locatie worden weergegeven door de waarde van de variabele Y. Rekening houdend met hoe een specifieke puntlocatie kan worden beschreven door een paar numerieke waarden op het oppervlak van een orthogonaal systeem, kunnen we de afstand tussen twee punten berekenen, evenals de richting van de rechte lijn gevormd door die twee punten, zoals aangetoond hieronder:
- D12 = [(X1 - X2) ^ 2 + (Y1 - Y2) ^ 2] ^ (1/2)
- TANa12 = [(Y1 - Y2) / (X1 - X2)]
- a12 = arcTAN [(X1-X2) / (Y1-Y2)]
Waarbij 1 en 2 twee gegeven punten op het oppervlak van het platte coördinatensysteem en (X1, Y1) & (X2, Y2) hun coördinaatwaarden vertegenwoordigen. Daarom vertegenwoordigt D12 de afstand tussen die twee punten en vertegenwoordigt a12 het hoekadres van de rechte lijn gevormd door die twee punten, zoals waargenomen bij het verplaatsen van punt 1 naar punt 2 . Het symbool TAN vertegenwoordigt een trigonometrische functie, dus om de waarde van de hoek a12 te schatten, moet men de arcTAN (of TAN ^ (- 1)) berekenen om de a12 te definiërende waarde van de hoek. Het is een trieste waarheid dat de ontwikkeling van alle hierboven beschreven methoden en de systematische weergave van coördinatensystemen op het oppervlak van toewijzingen werd veroorzaakt door de technologische vooruitgang van wapensystemen tijdens WO1. Berekeningen die geografische breedtegraad- en lengtegraadwaarden omvatten, waren te ingewikkeld om snelle slagveldberekeningen te dienen en daarom was de oprichting van het Flat Coordinate-systeem een praktische oplossing.

3D Cartesian Coordinate System./ Afbeeldingsbron: commons.wikimedia.org ( GNU Free Documentation License (Auteur: Gustavb )
Om samen te vatten, om een vlakke coördinaten te definiëren, moeten systeemingenieurs de referentiebol op een vlak oppervlak projecteren door de juiste cartografische projectie te gebruiken. Dan is het tijd om de primaire assen Ox en Oy te plaatsen en daarom het referentiepunt van het rastersysteem te bepalen waar de assen elkaar kruisen. Het rastersysteem van de kaart wordt later geconstrueerd door assen in gelijke delen te verdelen en absoluut parallelle lijnen te graveren die vierkanten met gelijke gebieden vormen op het oppervlak van de kaart. Waarnemers kunnen nu elke puntcoördinaat berekenen door de verticale afstand van het punt tot beide primaire assen te meten. Dit kan worden bereikt op elk niveau van gevraagde precisie en gemeten in elk metrisch systeem dat wordt gebruikt voor de berekening van afstanden op het natuurlijke aardoppervlak. Grapje, hoop het maar. :)
Grid-systemen
We zullen nu dieper ingaan op de belangrijkste vier van de verschillende Cartesiaanse coördinatenstelsels die tegenwoordig veel in de VS worden gebruikt en de 'Cartesiaanse' Grid-systemen die door die systemen worden gebruikt. Ik beloofde in de inleiding dat ik hier verder op in zou gaan en hier moet ik uitleggen dat ik die rastersystemen zojuist Cartesiaanse rastersystemen heb genoemd vanwege het feit dat de geometrische attributen zijn gebruikt en aangetoond, evenals de wiskundige functies die hun aard beschrijven en eigenschappen worden 'overgenomen' uit het Cartesiaanse coördinatensysteem en dus was de ontwikkeling van die netten waar we het over hebben op dit systeem gebaseerd. Dat verklaart waarom ik het tussen aanhalingstekens zet, ik speel gewoon zoals altijd met de betekenis van wetenschappelijke termen. Er zijn tegenwoordig vier hoofdtypen Grid-systemen, zoals hieronder wordt aangetoond:
- Universal Transverse Mercator Grid System (UTM)
Het Universal Transverse Mercator Grid System wordt tegenwoordig op grote schaal gebruikt in het geval van topografische afbeeldingen en satellietbeelden, evenals bij het creëren van allerlei soorten databases in het algemeen, inclusief informatie over verschillende soorten natuurlijke hulpbronnen en ruimtelijke verdeling correlaties tussen die. Het UTM-systeem wordt gebruikt in gevallen waarin hoge precisie met betrekking tot topologie vereist is en gebruikt de meter (m) als een meeteenheid met betrekking tot afstanden. Het UTM-rastersysteem is ontworpen en gebouwd met behulp van de Tranvserse Mercator-projectie. Je raadt het waarschijnlijk al. Het is vermeldenswaard dat het is ontworpen om te focussen op gebieden van het natuurlijke aardoppervlak die zich binnen de grenzen van respectievelijk de parallellen van 84N en 80S bevinden.
- Universeel Polar stereografisch rastersysteem (UPS)
Het Universal Polar Stereographic Grid System is ontworpen om te focussen op gebieden van het natuurlijke terrestrische oppervlak ten noorden van de parallel van 84N en ten zuiden van de parallelle van 80S, en biedt een coördinaten- en rastersysteem dat de precisieniveaus van de UTM kan bereiken. De richting van het noorden op het rooster is absoluut evenwijdig aan de richting van de centrale Meridiaan. Het is vermeldenswaard dat de rasterzones in het UPS-systeem zijn verdeeld in vierkanten met gelijke oppervlakte, net als in het geval van het UTM-systeem. Het UPS-rastersysteem is gebouwd met behulp van een versie van de stereografische azimutale projectie die is gecentreerd op de noordpool van de aarde. Dit geeft het UPS-rastersysteem het belangrijke kenmerk van het behoud van de schaalfactor in de richting van de parallellen. - State Plane Coordinate System (SPC)
Het State Plane Coordinate System is ontworpen en gemaakt door de US Coast and Geodetic Survey, die tegenwoordig bekend staat als de US Chart and Geodetic Survey, in de jaren dertig van de vorige eeuw. Ze hebben in feite een orthogonaal coördinatensysteem uitgevonden voor elk van de 50 staten om Surveying Engineers te helpen met het proces van driehoeksmeting, een techniek die wordt gebruikt om een systeem van punten met bekende coördinaten te maken dat de verdere studie en ontwikkeling zou helpen van het natuurlijke aardoppervlak. Het SPC-rastersysteem is gebaseerd op de Transverse Mercator-projectie, maar er zijn gevallen waarin de Lambert Conformal Conical Projection wordt gebruikt. - Public Land Survey System (PLSS)
Het Public Land Survey System werd ontworpen in 1785, nadat het Congres wetgeving had aangenomen voor de oprichting van een orthogonaal coördinatenstelsel dat breed zou worden gebruikt bij het maken van kaarten met betrekking tot de monumenten en het openbaar eigendom van het land. Het rastersysteem dat in de PLSS wordt gebruikt, vertoont fundamentele verschillen met die in de UTM- en UPS-systemen. De primaire meeteenheid die wordt gebruikt in de PLSS met betrekking tot oppervlakten is 1 hectare, wat overeenkomt met 10.000 m ^ 2. Tegenwoordig bestrijkt de PLSS gebieden van het natuurlijke aardoppervlak met meer dan 75% van het land in de 50 staten van Amerika. Berekeningen zijn echter vrij ingewikkeld vanwege het feit dat traditionele Amerikaanse meeteenheden worden gebruikt. 1 hectare is gelijk aan 43.560 vierkante voet of 1/640 vierkante mijl ...
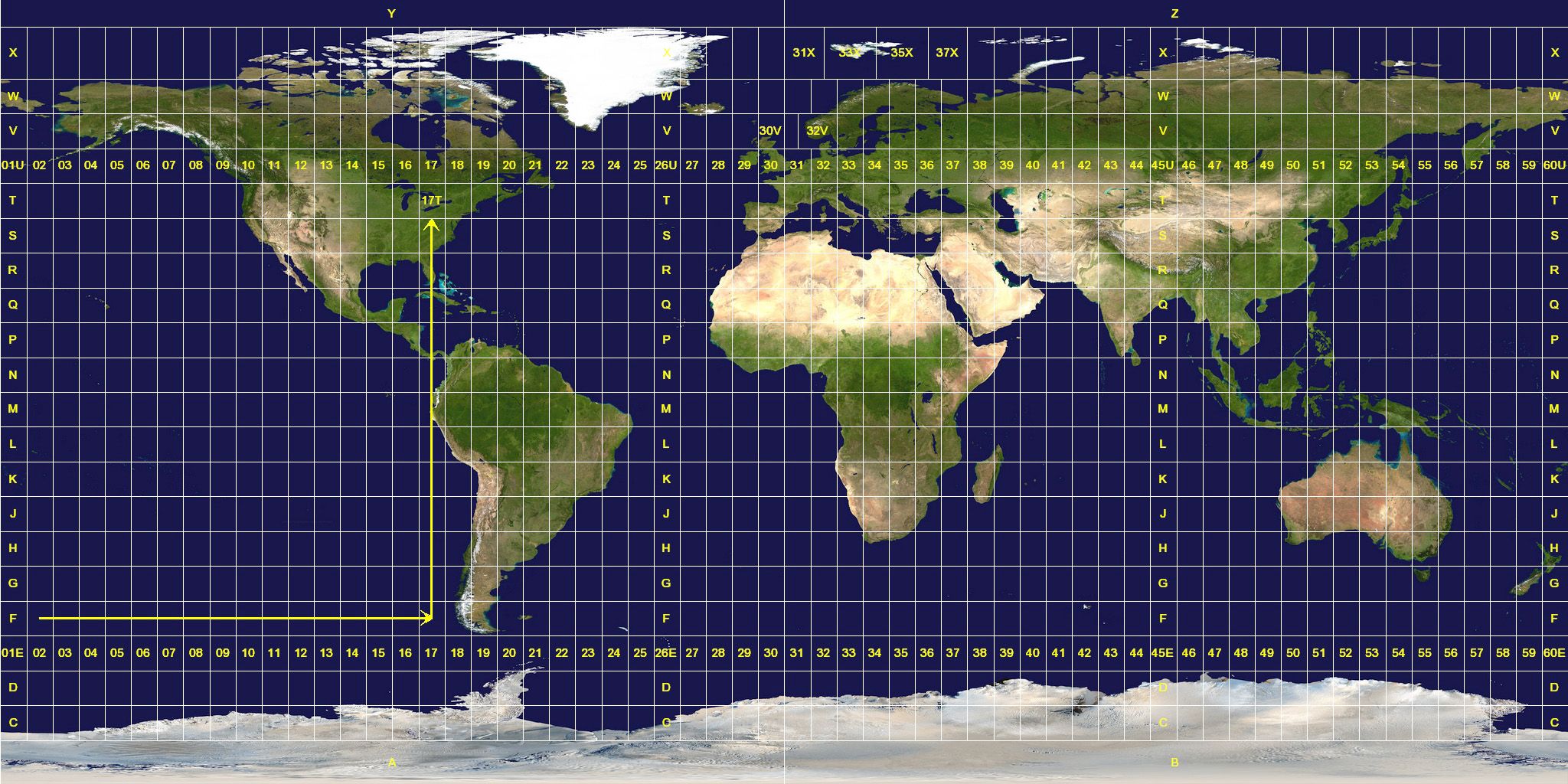
UTM Grid System./ Afbeeldingsbron: commons.wikimedia.org ( Public Domain Dedications (Auteur: NASA Earth Observatory )
Oke, dat is het voor vandaag jongens! Bedankt voor het langskomen van mijn blog en het nemen van de tijd om mijn werk te lezen. Ik hoop dat je dit net zo goed benijdde als ik. Dat gezegd hebbende, is het achtste deel van de serie Inleiding tot cartografie met betrekking tot Cartesiaanse coördinaten en rastersystemen ten einde. Laat het me weten in de reacties hieronder als je vragen hebt en ik zal mijn best doen om snel antwoorden te geven. Volg mij voor meer technische blogs! :)
VORIGE ONDERDELEN VAN DE REEKS:

BEELDBRONNEN:
Referenties:
Universitaire handboeken & cursuslezingen:
- Χαρτογραφία Ι / Cartography I -TSOULOS (National Technical University of Athens, School of Rural & Surveying Engineering, Course Lecture Notes)
- Στοιχεία Χαρτογραφίας, Πανεπιστημιακές Εκδόσεις Ε.Μ.Π. / Εlements of Cartography, Universitaire publicaties NTUA -AH ROBINSON, JL MORRISON, SC GUPTILL, University, PC, International University, PC GIRLINGON, AJ KIMERLING, AJ KIMERLING, University, PC Leerboek)
- Αναλυτική Χαρτογραφία, Πανεπιστημιακές Εκδόσεις Ε.Μ.Π. / Analytical Cartography, University Publications NTUA -NAKOS (National Technical University of Athens, School of Rural & Surveying Engineering, University Textbook)
Internet links:
Profile link : https://bitcointalk.org/index.php?action=profile;u=1523539;sa=forumProfile

Komentar
Posting Komentar